

This input excitation pulse is called input stimulus variable. In dynamic modeling, it is assumed that the system’s initial state is disturbed due to an external excitation or load change which forces the system to respond dynamically. Initial conditions affect the value of dynamic variables (state variables) at any time in the future. Generally, initial conditions are needed in order to be able to trace the changes in the system’s variables in time.

In mathematics and particularly in dynamic systems, an initial conditionis the value of an evolving variable at some specific point in time (typically denoted as t = 0). To simulate and predict a system’s dynamic response, all parameters and properties of the system which affect system inertia have to be known and considered. Obviously, the system’s dynamic response depends on its inherent inertia and also the input stimulus which causes the system to break through its initial steady-state condition. The inertia of a systemis defined by its tendency to remain unchanged or its resistivity against the variation. The basic concepts that have to be known in dynamic modeling include system inertia, initial condition, input stimulus variable, and time constant. Generally, the dynamic behavior of a system including mechanical, electrical, fluid, thermal, and so on can be described by a set of transient differential equations (ODE or PDE) which originates from the governing physical principals and inherent physical characteristics. A dynamic model is able to trace the variation of the system operating parameters in all operating conditions and consequently detect the critical points and outranges. The mathematical modeling of the dynamic systems and analysis of their dynamic characteristics is essential for developing the control and monitoring systems.
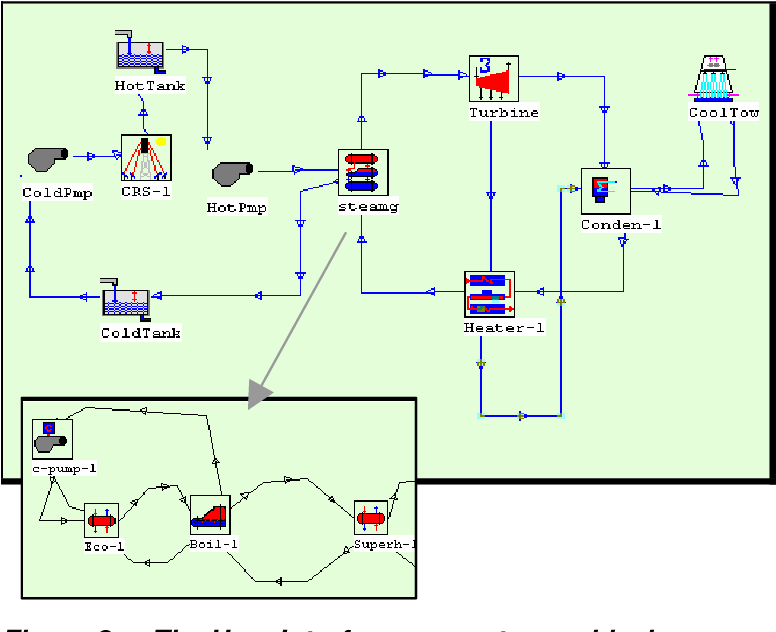
The aim of the chapter is to investigate and review the methodologies applicable for dynamic simulation of ORC power plants. Using dynamic models enables plant operators to predict changes in power output as a function of the plant’s boundary conditions such as temperature of the heat source and ambient conditions, so that they can respond to the expected heat and power demand accordingly. One example is the proportion of liquid and vapor phase in the condenser and evaporator that must be kept within acceptable ranges to avoid stalling or temperature shocks during transient conditions. The estimation of plant operating parameters during transient operation is crucial for monitoring and control of the plant so that the system state variables do not exceed the pre-defined operating range. Dynamic models are necessary for the better understanding of the plants’ behavior during transient operation, such as start-up, shutdown, and during rapid load changes. This chapter presents dynamic modeling approaches suitable for organic Rankine cycle (ORC) power plants.


 0 kommentar(er)
0 kommentar(er)
